利用神经网络拟合一元二次方程

我们这次要拟合的关系是一个一元二次方程

目标

• 理解参数初始化对于模型效果的重要影响。
• 学习模型训练过程中，如何通过观察损失值相应的调整学习率、epoch大小。

数据构建

这次我们在准备数据的时候，就将数据进行划分好，总训练集100个，训练集90个，测试集10个。

# 生成准备y = x^2 + 2x + 1数据，共100个点，并按9:1的比例划分为训练集和测试集,并保存到CSV文件
​
import numpy as np
​
from sklearn.model_selection import train_test_split
​
# 生成输入数据
x = np.linspace(-10, 10, 100) # 在[-10, 10]范围内生成100个均匀分布的点
​
# 生成目标输出数据
y = x**2 + 2 * x + 1
​
# 划分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.1, random_state=42)
​
# 保存训练集数据到CSV文件
train_data = np.column_stack((x_train, y_train))
​
np.savetxt('train.csv', train_data, delimiter=',', header='x,y', comments='')
​
# 保存测试集数据到CSV文件
test_data = np.column_stack((x_test, y_test))
​
np.savetxt('test.csv', test_data, delimiter=',', header='x,y', comments='')
​
print("数据保存成功！")

训练集准备好之后，得到train.csv和test.csv两个数据集，分布做训练和测试验证用。

现在开始构建神经网络，以拟合数据集中未知的关系。尽管我们清楚这个数据集是由一元二次方程生成的，但为了模拟实际情况，我们要有意地“忘掉”这一点。假设我们面对的是一个完全未知的数据集，不清楚其中的模式或潜在规律，这就要求我们不能直接进入模型构建环节，而是先对数据进行全面的探索和分析。

现在开始实验，此时我们面对的是(x,y)的数据点，但是并不知道他们的关系，目标是构建一个神经网络来拟合潜在关系。

数据探索与可视化

老规矩，先进行数据探索和数据可视化。

import matplotlib.pyplot as plt
​
# 读取data.csv文件到本地变量x和y中
import numpy as np
​
data = np.loadtxt('train.csv', delimiter=',', skiprows=1)
x = data[:, 0]
y = data[:, 1]
​
# 可视化数据
plt.scatter(x, y, color='green', label='data-exploit')
plt.xlabel('x')
plt.ylabel('y')
plt.title('data exploit')
plt.legend()
plt.show()

可以看到，(x,y)的关系并不是一个线性或近线性关系，因此用在构建模型的时候，不能直接用线性模型进行构建，而需要引入非线性部件，也就是隐含层和激活函数。

模型构造

# 定义模型方法，简单线性模型，无隐含层
def build_linear_model():
    model = keras.Sequential([
        layers.Dense(1, input_shape=(2,))  # 只有输出层
    ])
    return model

模型训练

为了能够清晰看到每轮epoch误差的走势，我们将误差进行可视化，按照理想的情况，误差应该是逐步降低，并且趋于一个较小的值。

在图中可以看到，轮次在1000左右，误差开始区域平稳，并没有下降了，而误差大小却还是900多，这也验证了在数据探索时看到的，这个数据集并不是一个简单的线性关系，线性模型无法很好的拟合，表现出来也是误差偏大

既然简单的线性模型误差偏大，那么就需要增加模型复杂度，增加隐藏层和激活函数，来拟合非线性关系

# 定义模型方法，包含隐含层，用pytorch的模型方法来定义
class LinearModel(nn.Module):
  def __init__(self):
    super(LinearModel, self).__init__()
    self.layer = nn.Sequential(
      nn.Linear(1, 16),
      nn.ReLU(),
      nn.Linear(16, 1)
    )
​
    def forward(self, x):
      return self.layer(x)
​
# 固定初始权重和偏置，例如权重为 0.5，偏置为 0.1
with torch.no_grad():
  model.layer[0].weight.fill_(0.5)
  model.layer[0].bias.fill_(0.1)
  model.layer[2].weight.fill_(0.5)
  model.layer[2].bias.fill_(0.1)

选择隐藏层中的单元（神经元）数量确实是一个重要的超参数，直接影响模型的表达能力和训练效果。没有固定的公式来选择最优的神经元数量，但可以考虑以下几方面来做出合理的选择：

• 简单任务：通常从 8、16 或 32 开始测试。如果在这些较小的神经元数量上表现良好，就不需要再增加。
• 非线性关系且复杂任务：可以尝试 32 或 64，但一般来说超过 64 会显得多余，尤其是在单层隐藏层的情况下。

逐步调试和验证

• 选择一个小的神经元数量（如 8 或 16），观察模型的表现。
• 更少的神经元数量意味着更少的参数，这会降低计算复杂度，提高训练速度，同时也能减少过拟合的风险。
• 在神经元数量过多时，模型可能学到数据中的噪声和细节，导致过拟合。

因为在数据探索可视化步骤中已经看到了数据的非线性关系，因此我们从16个神经元数量开始

激活函数Relu、学习率0.001、轮次100开始训练，并观测成本的走势

可以看到Loss一直是下降趋势，并没有到达一个平缓值，也没出现抖动，我们继续增加训练轮次到500

成本在300 epoch后下降趋势变得平缓，无法继续收敛，此时的损失输出。

可以看到模型Loss已经到达瓶颈，在300多处无法再下降了，此时模型还是处于误差偏大的情况，应该增加模型复杂度，我们先考虑增加隐藏层单元数，试试效果，将16增加到32

self.layer = nn.Sequential(
  nn.Linear(1, 32),
  nn.ReLU(),
  nn.Linear(32, 1)
)

损失快速下降，并且未出现瓶颈，继续增加epoch大小到1000。

epoch增加到1000看到下降趋势仍然明显，并且毫无平缓趋势，表示还未到达最小值附近，轮次虽然增加了一倍，但损失值没有显著降低，收敛速度较慢，因此将学习率从0.001调整为0.01，加速收敛过程，看看效果。

整体变化不大，继续调整0.01到0.1，加速收敛过程，看看效果。

效果非常明显，epoch在200左右开始，损失曲线进入平滑，但是此时损失值还在300以上，虽然效果并不是很好，但是以上对于学习率的尝试，可以感受到对收敛速度的影响。

面对这个损失值趋于平缓，且值较大，会猜测是否是学习率过大，导致未能很好的收敛至最小值，或者是模型复杂度不够，无法表达出数据的复杂关系。

先来验证第一个猜想，降低学习率，并且增大epoch次数，让模型在较小的学习率上，足够轮次去学习，看看能收敛到什么效果。尝试多轮试验，在0.001的学习率，epoch为30000时，足够小的学习率和足够多的轮次，损失曲线走向平缓，但是可以看到，损失值还是在300以上，足以验证并非时学习率导致未能收敛至最小值。

再来验证第二个猜想，增加模型复杂度，增加一个隐藏层。

self.layer = nn.Sequential(
    nn.Linear(1, 64),
    nn.ReLU(),
    nn.Linear(64, 1)
)

Loss值依然很大，单纯通过增加隐藏层单元数作用不大。

考虑继续增加模型复杂度，增加隐藏层数量，从一个隐藏层增加到两个隐藏层

self.layer = nn.Sequential(
    nn.Linear(1, 32),
    nn.ReLU(),
    nn.Linear(32, 16),
    nn.ReLU(),
    nn.Linear(16, 1)
)

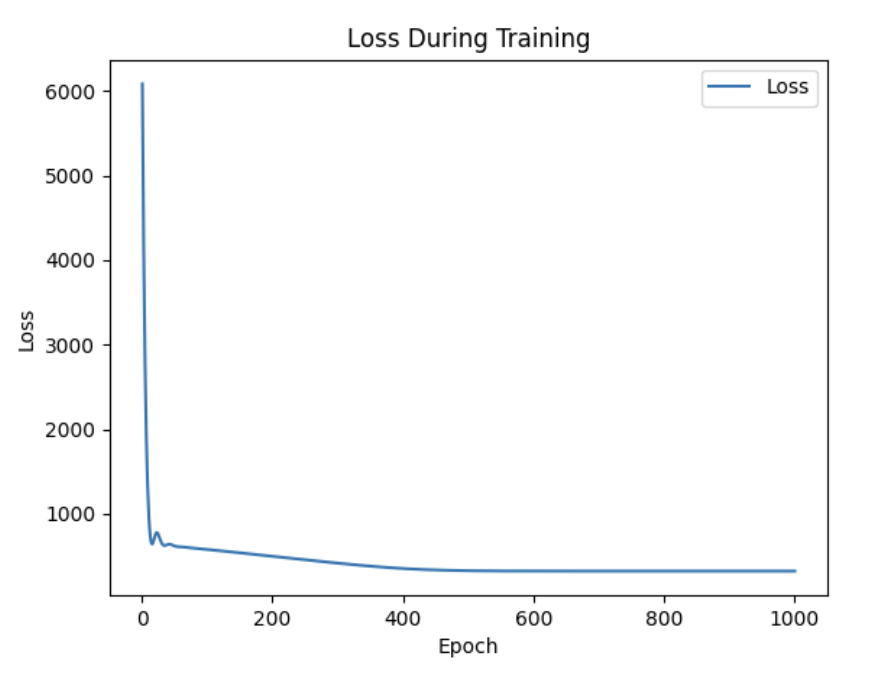
损失值依然还是处于高水位。

我们通过改变学习率、神经单元数，对Loss值的改变都没什么作用，陷入沉思。

仔细思考我们的模型，会发现，模型的初始化参数时手动设置的。

# 固定初始权重和偏置，例如权重为 0.5，偏置为 0.1
with torch.no_grad():
    model.layer[0].weight.fill_(0.5)
    model.layer[0].bias.fill_(0.1)
    model.layer[2].weight.fill_(0.5)
    model.layer[2].bias.fill_(0.1)

仔细思考，会发现手动初始化参数会有一个问题，每层所有的神经单元权重和更新都是一样的，只是一个单元的复制，因此无论单元数是8，还是64，本质都只是1，模型的表达能力大大退化，无法展示出复杂的表达能力。

恍然大悟，通过随机初始权重来替代手动初始化，用最初最简单的模型结构训练，看看效果

# 使用随机初始化的方法，替代 np.full 的固定值
self.layer = nn.Sequential(
    nn.Linear(1, 64),
    nn.ReLU(),
    nn.Linear(64, 1)
)
# 注释掉手动设置参数的逻辑
# with torch.no_grad():
#     model.layer[0].weight.fill_(0.5)
#     model.layer[0].bias.fill_(0.1)
#     model.layer[2].weight.fill_(0.5)
#     model.layer[2].bias.fill_(0.1)

Final Loss效果十分明显，证实我们的猜想是正确的。我们通过自动初始化，即如He初始化或Xavier初始化

之前设置的偏重和权重数是随意设置的，偏重0.5、0.1，现在不自己设置，改为由自动生成，看看效果

很神奇的一幕出现了，Loss居然一下子到达了从323多下降到0.24，效果惊人。

正常的梯度值应该是：

某一层的平均梯度可能从最初的较大值（比如 0.1 - 1）逐渐减小到 0.01 - 0.1 左右，随着训练的进行波动幅度也逐渐缩小。

注意一个情况，即每次运行可能得到的Final Loss值会不一样，原因是模型中存在几个随机给变量，分别是：Adam动量、随机初始化权重、偏重。这些都是影响模型效果的变量，面对随机变量，只要设定一个目标值，达到目标值之后就可以将模型保存。

面对当前目标，我们认为final loss在1以下就是可以接受的范围，这里没有一个定论，而是要与你实际的场景相结合，当目前final loss = 0.2，由于我损失函数用的是mean_squared_error，0.2开根号= 0.45，即预测误差会在大约0.45范围，这个是我可以接受的范围。

测试验证

接下来就是在测试环境进行模型验证：

# 测试集验证
import torch
from nonlinear_train_pt import NonLinearModel
import numpy as np
import torch.nn as nn

# 从data.csv文件中读取数据
def load_data(file_path):
    data = np.loadtxt(file_path, delimiter=',', skiprows=1)
    x = data[:, 0]
    y = data[:, 1]
    return x, y

if __name__ == "__main__":
    # 加载数据
    x, y = load_data('test.csv')
    x = torch.tensor(x, dtype=torch.float32).view(-1, 1)
    y = torch.tensor(y, dtype=torch.float32).view(-1, 1)

    # 加载模型
    model = NonLinearModel()
    model.load_state_dict(torch.load("nonlinear_model.pth", weights_only=True))
    criterion = nn.MSELoss()
    # 训练后评估模型
    model.eval()
    final_loss = criterion(model(x), y).item()
    print(f"Test final loss: {final_loss}")

Final Loss一下退后了好几个小数点，效果十分显著。

在测试集上进行验证，注意，模型是在标准后的数据上进行训练得到的，因此测试验证时，也需要利用训练数据的标准化参数进行处理。

运行之后得到结果发现，在标准化后的数据上效果很好，但是在真实数据集上去衡量，效果却远达不到。从下图可以看到，利用标准化数据进行预测，Loss在0.00138、而在真实值上预测，却在1.22，差了很多

总结

整体思路（从简单到复杂，更简单的模型部署、推理成本更低）：

数据探索可视化 -> 非线性模型 -> 2层 -> 调整轮次、学习率 ->效果不佳 -> 自动初始化 -> 效果变好 -> 继续优化，数据标准化 ->标准化测试效果好，但真实值效果不好 -> 不用标准化，增加模型层数到3层 ->效果达标。